Error with Reversing an Integer( Leetcode 7. Reverse Integer) & its solution

908



First, let's understand what this problem is saying.

To understand how the number 2147483647 fits in a 32-bit signed integer and how overflow can occur, let's break it down step-by-step.

1. Understanding 32-bit Signed Integers

A signed 32-bit integer can represent values in the range of ([-2^{31}, 2^{31} - 1]). This is because one bit is used for the sign (positive or negative), leaving 31 bits for the value itself.

  • Maximum Value: (2^{31} - 1 = 2147483647)
  • Minimum Value: (-2^{31} = -2147483648)

2. Binary Representation of 2147483647

To see how 2147483647 fits in 32 bits, we can look at its binary representation:

  • Decimal: 2147483647
  • Binary: 01111111111111111111111111111111

This binary number has:

  • 31 bits for the value (all set to 1)
  • 1 bit for the sign (0, indicating a positive number)

3. Reversing an Integer

When reversing an integer, you manipulate its digits. For example, reversing 123 gives you 321. However, if you reverse 2147483647, you get 7463847412, which exceeds the maximum value of a signed 32-bit integer.

4. Overflow Explanation

Overflow occurs when a calculation produces a result that is outside the range that can be represented with the available bits. In the case of reversing integers:

  • If the reversed integer exceeds 2147483647, it cannot be stored in a signed 32-bit integer.
  • The problem statement specifies that if reversing the integer causes it to go outside the range ([-2^{31}, 2^{31} - 1]), you should return 0.

5. Example of Overflow

  • Input: 2147483647
  • Reversed: 7463847412 (which is greater than 2147483647)
  • Output: 0 (because it overflows)

Summary

  • A signed 32-bit integer can represent values from (-2147483648) to (2147483647).
  • The number 2147483647 is the maximum positive value and is represented in binary as 01111111111111111111111111111111.
  • Reversing certain integers can lead to values that exceed this range, resulting in overflow, which is handled by returning 0.

Now, Let’s dive deeper into the key concepts behind the issues and logic for the "Reverse Integer" problem to enhance our understanding.

Issues with our Original Solution(in the picture)

  1. Overflow Handling:

    • Understanding Overflow: In programming, overflow occurs when an operation results in a value that exceeds the maximum limit of the data type being used. For a 32-bit signed integer, the valid range is from (-2^{31}) (which is -2147483648) to (2^{31} - 1) (which is 2147483647).
    • Why It Matters: When reversing the integer, digits are added to the new integer (ans) one by one. If the reversed integer exceeds these bounds at any point, it could lead to incorrect results. For example, reversing 1534236469 would yield 9646324351, which is out of bounds.
    • Returning 0: The problem specifies that in case of overflow, you should return 0 instead of the invalid reversed number.

  2. Incorrect Initialization:

    • Starting Point: Initializing ans to 0 is appropriate as it ensures you start building your reversed number from a neutral point. However, incorrect handling down the line can create scenarios where ans might exceed bounds before you can check it.
    • Updating ans Incorrectly: It's important to ensure that ans is updated in a safe way so that it does not create an invalid state.

  3. Digit Extraction:

    • Modular Arithmetic: Using x % 10 effectively extracts the last digit of x, which is a correct approach. Reducing x using x /= 10 properly shifts the number left, making it ready for the next loop.
    • Potential Issue: However, if you do not check for overflow right after you calculate the new ans, you could end up with an invalid value.

The Correct Solution

Now let’s break down the correct solution step by step.

Code Overview

class Solution {
public:
    int reverse(int x) {
        int ans = 0;
        while (x) {
            int digit = x % 10; // Get the last digit
            
            // Check for overflow before updating ans
            if (ans > INT_MAX / 10 || (ans == INT_MAX / 10 && digit > 7)) return 0; // Overflow for positive
            if (ans < INT_MIN / 10 || (ans == INT_MIN / 10 && digit < -8)) return 0; // Overflow for negative
            
            ans = ans * 10 + digit; // Update ans
            x /= 10; // Remove the last digit from x
        }
        return ans;
    }
};

Logic Behind the Solution

  1. Digit Extraction:

    • The line int digit = x % 10 extracts the last digit of the number x. For example, if x is 123, digit will be 3.
    • x /= 10; effectively removes this last digit by integer division. For example, after this operation, x becomes 12.

  2. Overflow Check:

    • Prevention Logic:
      • When preparing to update ans, it's vital to ensure that multiplying ans by 10 (to shift its digits left) won’t cause an overflow.
      • The condition ans > INT_MAX / 10 checks if multiplying ans by 10 might exceed the maximum integer.
      • If ans == INT_MAX / 10, it means we are at the edge of the limit. We then check if digit > 7, because with a maximum integer of 2147483647, its last digit is 7. If digit exceeds 7, we can safely say that ans will overflow.
    • Negative Check:
      • The same logic applies for negative integers, but with adjusted limits based on INT_MIN. Here, INT_MIN is (-2147483648) and hence its last digit consideration is -8.

(#### Find the derivations of these conditions at the end of this explainer)

  1. Final Return:
    • After all iterations and calculations, if the number has been safely reversed without any risk of overflow, the reversed integer ans is returned.

Summary of Key Principles:

  • Always Check for Overflow: This is critical in any arithmetic operation where limits could be breached.
  • Modular Arithmetic for Extraction: Using % allows for clean digit extraction and shifting digits correctly.
  • Consider Both Sign Cases: Make sure to check the conditions for both positive and negative integers when defining overflow logic.

In conclusion, understanding these principles not only helps in solving the "Reverse Integer" problem but also greatly enhances your problem-solving skills across other similar challenges in coding.

ℹ️ #### Explanation/Derivation of the conditional statements:

Let’s clarify this point with a bit more detail on why and how the digit impacts both positive and negative overflow checks.

Constructing the Logic with digit

When we're reversing the integer, each step involves both multiplying the current ans by 10 (to shift its digits left) and adding the next digit. This means we need to not only check the current value of ans but also account for the next digit being added. Let’s break it down further.

Overflow Conditions for Positive Integers

  1. Basic Check Before Multiplying:
    • First, we prevent ans from exceeding the maximum allowable integer value after shifting left. Therefore, the first part of our condition:

  • This check ensures multiplying ans by 10 will not exceed INT_MAX.
  1. Checking After Multiplication & Adding digit:
    • If ans is exactly INT_MAX / 10, we still need to check that the digit we are about to add does not push ans over INT_MAX. This yields the second part of the overflow check:

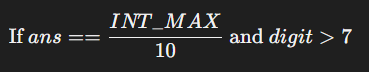
  • Since 7 is the highest digit in 2147483647, adding any digit greater than 7 would exceed the maximum limit when combined with ans.

Overflow Conditions for Negative Integers

  1. Basic Check Before Multiplying:
    • For negative numbers, we want to prevent ans from becoming more negative than INT_MIN:

  • This means multiplying ans by 10 will definitely result in a value less than INT_MIN.
  1. Checking After Multiplication & Adding digit:
    • If ans is already INT_MIN / 10, we need to ensure that the next digit we add will not take it beyond the minimum:

  • The -8 is derived from the number -2147483648, where the smallest digit can only be -8. Adding any digit less than -8 would move us below the limit.

Summary of the Importance of digit

The logic for considering digit in these overflow checks is essential:

  • Determining Safety: The checks with digit specifically ensure that while we are incrementally building the reversed integer, the combined operation of shifting and adding the digit remains within safe boundaries.

  • Prevention of Overflow and Underflow: Without taking digit into account, we might incorrectly allow an operation that results in an invalid integer value.

Thus, including digit in the conditional checks is critical to ensure correct and safe computation while reversing the integer. The checks ensure that we account for all potential paths that the operation may take and stay within the constraints of the 32-bit signed integer range.

🤗Let's perform a detailed step-by-step dry run of the reverse function using two examples: one that causes an overflow and another that causes an underflow. This will help illustrate the logic and intuition behind the code.

Example 1: Overflow Case

Input: x = 1534236469

Initialization:

  • ans = 0
  • x = 1534236469

Step-by-Step Iteration:

  1. First Iteration:

    • digit = 1534236469 % 10 = 9
    • Check for overflow:
      • ans > INT_MAX / 10 → 0 > 214748364 (false)
      • ans == INT_MAX / 10 → 0 == 214748364 (false)
    • Update ans: ans = 0 * 10 + 9 = 9
    • Update x: x = 1534236469 / 10 = 153423646

  2. Second Iteration:

    • digit = 153423646 % 10 = 6
    • Check for overflow:
      • ans > INT_MAX / 10 → 9 > 214748364 (false)
      • ans == INT_MAX / 10 → 9 == 214748364 (false)
    • Update ans: ans = 9 * 10 + 6 = 96
    • Update x: x = 153423646 / 10 = 15342364

  3. Third Iteration:

    • digit = 15342364 % 10 = 4
    • Check for overflow:
      • ans > INT_MAX / 10 → 96 > 214748364 (false)
      • ans == INT_MAX / 10 → 96 == 214748364 (false)
    • Update ans: ans = 96 * 10 + 4 = 964
    • Update x: x = 15342364 / 10 = 1534236

  4. Fourth Iteration:

    • digit = 1534236 % 10 = 6
    • Check for overflow:
      • ans > INT_MAX / 10 → 964 > 214748364 (false)
      • ans == INT_MAX / 10 → 964 == 214748364 (false)
    • Update ans: ans = 964 * 10 + 6 = 9646
    • Update x: x = 1534236 / 10 = 153423

  5. Fifth Iteration:

    • digit = 153423 % 10 = 3
    • Check for overflow:
      • ans > INT_MAX / 10 → 9646 > 214748364 (false)
      • ans == INT_MAX / 10 → 9646 == 214748364 (false)
    • Update ans: ans = 9646 * 10 + 3 = 96463
    • Update x: x = 153423 / 10 = 15342

  6. Sixth Iteration:

    • digit = 15342 % 10 = 2
    • Check for overflow:
      • ans > INT_MAX / 10 → 96463 > 214748364 (false)
      • ans == INT_MAX / 10 → 96463 == 214748364 (false)
    • Update ans: ans = 96463 * 10 + 2 = 964632
    • Update x: x = 15342 / 10 = 1534

  7. Seventh Iteration:

    • digit = 1534 % 10 = 4
    • Check for overflow:
      • ans > INT_MAX / 10 → 964632 > 214748364 (false)
      • ans == INT_MAX / 10 → 964632 == 214748364 (false)
    • Update ans: ans = 964632 * 10 + 4 = 9646324
    • Update x: x = 1534 / 10 = 153

  8. Eighth Iteration:

    • digit = 153 % 10 = 3
    • Check for overflow:
      • ans > INT_MAX / 10 → 9646324 > 214748364 (false)
      • ans == INT_MAX / 10 → 9646324 == 214748364 (false)
    • Update ans: ans = 9646324 * 10 + 3 = 96463243
    • Update x: x = 153 / 10 = 15

  9. Ninth Iteration:

    • digit = 15 % 10 = 5
    • Check for overflow:
      • ans > INT_MAX / 10 → 96463243 > 214748364 (false)
      • ans == INT_MAX / 10 → 96463243 == 214748364 (false)
    • Update ans: ans = 96463243 * 10 + 5 = 964632435
    • Update x: x = 15 / 10 = 1

  10. Tenth Iteration:

    • digit = 1 % 10 = 1
    • Check for overflow:
      • ans > INT_MAX / 10 → 964632435 > 214748364 (true)
    • Since this condition is true, the function returns 0 due to overflow.

Example 2: Underflow Case

Input: x = -2147483648

Initialization:

  • ans = 0
  • x = -2147483648

Step-by-Step Iteration:

  1. First Iteration:

    • digit = -2147483648 % 10 = -8
    • Check for underflow:
      • ans < INT_MIN / 10 → 0 < -214748364 (false)
      • ans == INT_MIN / 10 → 0 == -214748364 (false)
    • Update ans: ans = 0 * 10 - 8 = -8
    • Update x: x = -2147483648 / 10 = -214748364

  2. Second Iteration:

    • digit = -214748364 % 10 = -4
    • Check for underflow:
      • ans < INT_MIN / 10 → -8 < -214748364 (false)
      • ans == INT_MIN / 10 → -8 == -214748364 (false)
    • Update ans: ans = -8 * 10 - 4 = -84
    • Update x: x = -214748364 / 10 = -21474836

  3. Third Iteration:

    • digit = -21474836 % 10 = -6
    • Check for underflow:
      • ans < INT_MIN / 10 → -84 < -214748364 (false)
      • ans == INT_MIN / 10 → -84 == -214748364 (false)
    • Update ans: ans = -84 * 10 - 6 = -846
    • Update x: x = -21474836 / 10 = -2147483

  4. Fourth Iteration:

    • digit = -2147483 % 10 = -3
    • Check for underflow:
      • ans < INT_MIN / 10 → -846 < -214748364 (false)
      • ans == INT_MIN / 10 → -846 == -214748364 (false)
    • Update ans: ans = -846 * 10 - 3 = -8463
    • Update x: x = -2147483 / 10 = -214748

  5. Fifth Iteration:

    • digit = -214748 % 10 = -8
    • Check for underflow:
      • ans < INT_MIN / 10 → -8463 < -214748364 (false)
      • ans == INT_MIN / 10 → -8463 == -214748364 (false)
    • Update ans: ans = -8463 * 10 - 8 = -84638
    • Update x: x = -214748 / 10 = -21474

  6. Sixth Iteration:

    • digit = -21474 % 10 = -4
    • Check for underflow:
      • ans < INT_MIN / 10 → -84638 < -214748364 (false)
      • ans == INT_MIN / 10 → -84638 == -214748364 (false)
    • Update ans: ans = -84638 * 10 - 4 = -846384
    • Update x: x = -21474 / 10 = -2147

  7. Seventh Iteration:

    • digit = -2147 % 10 = -7
    • Check for underflow:
      • ans < INT_MIN / 10 → -846384 < -214748364 (false)
      • ans == INT_MIN / 10 → -846384 == -214748364 (false)
    • Update ans: ans = -846384 * 10 - 7 = -8463847
    • Update x: x = -2147 / 10 = -214

  8. Eighth Iteration:

    • digit = -214 % 10 = -4
    • Check for underflow:
      • ans < INT_MIN / 10 → -8463847 < -214748364 (false)
      • ans == INT_MIN / 10 → -8463847 == -214748364 (false)
    • Update ans: ans = -8463847 * 10 - 4 = -84638474
    • Update x: x = -214 / 10 = -21

  9. Ninth Iteration:

    • digit = -21 % 10 = -1
    • Check for underflow:
      • ans < INT_MIN / 10 → -84638474 < -214748364 (false)
      • ans == INT_MIN / 10 → -84638474 == -214748364 (false)
    • Update ans: ans = -84638474 * 10 - 1 = -846384741
    • Update x: x = -21 / 10 = -2

  10. Tenth Iteration:

    • digit = -2 % 10 = -2
    • Check for underflow:
      • ans < INT_MIN / 10 → -846384741 < -214748364 (true)
    • Since this condition is true, the function returns 0 due to underflow.

The dry run illustrates how the function processes each digit of the input integer, updating the result while checking for overflow and underflow conditions. This careful checking ensures that the function behaves correctly for large positive and negative integers, returning 0 when the reversed integer exceeds the bounds of a 32-bit signed integer.

😎Checking for overflow before processing the last digit is crucial for preventing the function from producing an incorrect result or crashing due to exceeding the limits of a 32-bit signed integer. Here's why this approach is necessary:

Reasons for Preemptive Overflow Check

Preventing Invalid States: If we only check for overflow after adding the last digit, we might end up with an invalid state where the result exceeds the maximum or minimum bounds of a 32-bit signed integer. This could lead to undefined behavior or incorrect results.

Immediate Feedback: By checking for overflow before updating the result, we can immediately determine if the next operation will lead to an overflow. This allows us to return a safe value (like 0) without performing any invalid calculations.

Efficiency: Checking for overflow beforehand avoids unnecessary calculations. If we know that adding the next digit will cause an overflow, we can skip the addition entirely and return the appropriate result.

🤔What Would Happen If We Checked After?

If we were to check for overflow only after attempting to add the last digit, the following issues could arise:

Incorrect Result: The function might return a value that exceeds the bounds of a 32-bit signed integer, leading to incorrect results. For example, if the result is calculated as 2147483648, it would wrap around to -2147483648 due to integer overflow.

Potential Crashes: In some programming environments, attempting to store a value that exceeds the maximum limit could lead to runtime errors or crashes, especially if the language does not handle integer overflow gracefully.

Loss of Control: The logic of the function would become less predictable. Instead of having a clear mechanism to handle overflow, it would rely on the behavior of the underlying integer representation, which can vary between programming languages and environments.

By checking for overflow before processing the last digit, we ensure that the function behaves predictably and safely. This approach allows us to maintain control over the output and avoid invalid states, ensuring that the function adheres to the constraints of a 32-bit signed integer.

🥳Let's perform a detailed dry run of the reverse function with the input x = 2147483638, which is chosen because its reversal will cause an overflow for a 32-bit signed integer.

Input:

x = 2147483638

Initialization:

  • ans = 0
  • x = 2147483638
  • INT_MAX = 2147483647 (maximum value for a 32-bit signed integer)

Step-by-Step Iteration:

  1. First Iteration:

    • digit = 2147483638 % 10 = 8
    • Check for overflow:
      • ans > INT_MAX / 10 → 0 > 214748364 (false)
      • ans == INT_MAX / 10 → 0 == 214748364 (false)
    • Update ans: ans = 0 * 10 + 8 = 8
    • Update x: x = 2147483638 / 10 = 214748363

  2. Second Iteration:

    • digit = 214748363 % 10 = 3
    • Check for overflow:
      • ans > INT_MAX / 10 → 8 > 214748364 (false)
      • ans == INT_MAX / 10 → 8 == 214748364 (false)
    • Update ans: ans = 8 * 10 + 3 = 83
    • Update x: x = 214748363 / 10 = 21474836

  3. Third Iteration:

    • digit = 21474836 % 10 = 6
    • Check for overflow:
      • ans > INT_MAX / 10 → 83 > 214748364 (false)
      • ans == INT_MAX / 10 → 83 == 214748364 (false)
    • Update ans: ans = 83 * 10 + 6 = 836
    • Update x: x = 21474836 / 10 = 2147483

  4. Fourth Iteration:

    • digit = 2147483 % 10 = 3
    • Check for overflow:
      • ans > INT_MAX / 10 → 836 > 214748364 (false)
      • ans == INT_MAX / 10 → 836 == 214748364 (false)
    • Update ans: ans = 836 * 10 + 3 = 8363
    • Update x: x = 2147483 / 10 = 214748

  5. Fifth Iteration:

    • digit = 214748 % 10 = 8
    • Check for overflow:
      • ans > INT_MAX / 10 → 8363 > 214748364 (false)
      • ans == INT_MAX / 10 → 8363 == 214748364 (false)
    • Update ans: ans = 8363 * 10 + 8 = 83638
    • Update x: x = 214748 / 10 = 21474

  6. Sixth Iteration:

    • digit = 21474 % 10 = 4
    • Check for overflow:
      • ans > INT_MAX / 10 → 83638 > 214748364 (false)
      • ans == INT_MAX / 10 → 83638 == 214748364 (false)
    • Update ans: ans = 83638 * 10 + 4 = 836384
    • Update x: x = 21474 / 10 = 2147

  7. Seventh Iteration:

    • digit = 2147 % 10 = 7
    • Check for overflow:
      • ans > INT_MAX / 10 → 836384 > 214748364 (false)
      • ans == INT_MAX / 10 → 836384 == 214748364 (false)
    • Update ans: ans = 836384 * 10 + 7 = 8363847
    • Update x: x = 2147 / 10 = 214

  8. Eighth Iteration:

    • digit = 214 % 10 = 4
    • Check for overflow:
      • ans > INT_MAX / 10 → 8363847 > 214748364 (false)
      • ans == INT_MAX / 10 → 8363847 == 214748364 (false)
    • Update ans: ans = 8363847 * 10 + 4 = 83638474
    • Update x: x = 214 / 10 = 21

  9. Ninth Iteration:

    • digit = 21 % 10 = 1
    • Check for overflow:
      • ans > INT_MAX / 10 → 83638474 > 214748364 (false)
      • ans == INT_MAX / 10 → 83638474 == 214748364 (false)
    • Update ans: ans = 83638474 * 10 + 1 = 836384741
    • Update x: x = 21 / 10 = 2

  10. Tenth Iteration:

    • digit = 2 % 10 = 2
    • Check for overflow:
      • ans > INT_MAX / 10 → 836384741 > 214748364 (true)
    • Since this condition is true, the function returns 0 due to overflow.

Conclusion

In this dry run, we see that after processing all digits of 2147483638, we reach ans = 836384741 and the next operation checks if adding another digit (2) would cause overflow. Since it would, the function correctly returns 0. Therefore, this input exemplifies how the reverse function handles integers close to the limits of 32-bit signed integer overflow.